51 氟-18氟化鈉(sodium fluoride)可用於何種器官之掃描？ (A)心臟 (D)肝臟 (C)腎臟 (D)骨骼

F-18用於骨骼掃描大概是緣起於1940年左右，不過由於當時迴旋加速器的不普遍以及攝影機的不夠精良，因此很快的骨骼掃描就都是使用Tc-99m的磷酸鹽，一直到了現在PET已經非常普及，F-18的取得也容易多了，才又逐漸使用F-18來作bone scan，F-18在注射後骨骼的攝取率相當的高，加上影像品質相當的好，和Tc-99m磷酸鹽分布的影像又幾乎相同，因此如果不考慮檢查所需支付的高額費用，F-18的確是作骨骼掃描的最佳藥劑，不但解析度好，又同時有3D的影像，其實F-18的藥物成本因為不若F-18 FDG還需經過合成的過程，因此在藥劑的成本上其實並不高，加上因為骨骼的攝取率很高，照相的時間就不用太久，不會排擠到高價格的F-18 FDG癌症掃描，因此我想在不久的將來，F-18應該會正式使用在骨骼掃描上，而且收費也會合理化，這是我們所樂見的。

52 鎵-67掃描時，閃爍攝影機不得配備何種準直儀？ (A)低能量 (B)中能量 (C)高能量 (D)針孔

Ga-67的能峰位於93(37%)、185(20.4%)以及300 KeV(16.6%)，它的能峰多半是屬於中能量的範圍，因此在造影時必須使用中能量的準直儀才能有比較好的影像表現，如果使用了(C)高能量的準直儀原則上也是可以，但是因為鉛隔太厚導致準直儀上面能容納的孔洞太少，影像的計數率會下降而且看起來會有蜂窩狀的感覺(鉛隔的形狀)，如果使用(D)針孔是沒問題的，只是因為針孔式準直儀一樣會有計數率很低的情形，這必須增加影像收集的時間才形，不過影像應該會蠻不錯的，只是視野會比較小就是了，至於(A)低能量準直儀就真的不行了，因為它的鉛隔太薄，因此影像的散射會很厲害，這部分的影像可以參考93年第2次檢覈考第40題。

53 利用FDG進行腦部掃描，在注射後、造影前，病患應躺在何種房間？ (A)一般檢查室 (B)無光線，有聲音的房間 (C)有光線，無聲音的房間 (D)無光線，無聲音的房間

利用FDG進行腦部掃描就是要觀察腦部的新陳代謝情形，它主要是用於偵測腦部腫瘤、腦血管障礙、退化性或癡呆症病變的早期診斷以及癲癇等等，事實上F-18 FDG最早期的研究都是集中在腦部的檢查，直到後來才逐漸轉移重心到癌症的掃描，由於惡性腫瘤利用葡萄糖的比率常遠超過良性腫瘤及正常的細胞，因此測量腦內細胞的葡萄糖利用狀態，可以分辨出良性腫瘤、惡性腫瘤與正常的腦細胞。因此當進行FDG腦部掃描時必須儘可能的降低腦部受到外來干擾的機會，譬如說過強的光線引起視覺區的活化等等，這一點和我們在做HMPAO的腦部掃描一樣，都必須讓病患處於安靜的環境下進行藥物的注射，因此這題的答案是(D)無光線，無聲音的房間。

54 一般放射免疫分析用之伽傌計數器所測檢體之體積約在什麼範圍？ (A)1～5mL (B)5～10mL (C)10～15mL (D)15～20mL

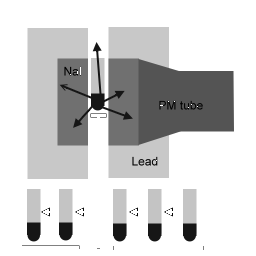
一般使用井型計數器所使用的碘化鈉多半是一個單一的晶體，在其中的一端挖有一個洞供測量檢體用(如圖)，最常使用標準的晶體大小直徑為4.5公分，高度為5公分，裡頭的洞直徑為1.6公分，深度為3.8公分，外頭包有5公分厚的鉛以減少背景值，由於NaI井型計數器的偵測效率相當高，背景值又低，因此很適合用來作為小活度物質的計數之用，在測量物的體積小於等於1 mL時它的幾何效率大約為93%，從另一個角度來說，如果檢體置於well-counter的底部，那麼溢漏未被偵測到的γ-ray約為7%，而如果置於洞口的話，就會有將近50%會偵測不到，因此如果說相同活度不同體積的檢體在同一台well-counter測量的話，體積較大的檢體會因為靠近洞口的部分較多，而導致溢漏出去的γ-ray也會比較多，造成計數值的減少，同樣的如果將活度的溶液不斷加入試管中去計數的話，一開始測量值會隨活度的增加而呈直線增加，可是隨著體積越來越大，溢漏出的γ-ray越多，最後計數值就不再會呈直線增加，而會比實際值略低，為了預防這件事的發生，RIA廠商在設計檢查試劑時，都會將最候要送進counter試管裡溶液的體積控制在1 mL以內，以避免此情形的發生，以上所提的皆是well-counter的數據，真正核醫RIA在使用的多半是連續型的伽傌計數器，也就是裡面的碘化鈉晶體不再是井型的，而是所謂的throuth-hole型的(如圖)，這樣除了提高工作效率外，因為機器手臂會自動將檢體推送到晶體的最中央，因此它的幾何效率不會因為檢體的體積增加而有太大變化，不過由於它的上下都有洞，因此背景值會偏高，而且較容易受到其他檢體的活度干擾，以上的資料是來自於Physics in Nuclear Medicine 第3版，作者是Simin R.Cherry，James A.Sorenson，Michael E. Phelps，出版社是SAUNDERS，綜合的來說，檢體的體積必須控制在1 mL左右，所以答案是(A)1～5mL。

Well-type	Through-hole

55 井型計數器(well counter)將其計數之標本涵蓋於其偵測範圍內，其counting geometry 為： (A)1π (B)2π (C)3π (D)4π

一個偵測器的偵測效率就是儀器能將射源所發射出的能量轉換成可用訊號的能力，所謂的偵測效率可以分為以下4個部分，1.geometry efficiency幾何效率，就是偵測器能夠包含住射源的效率，這跟偵測器的大小以及與射源之間的距離有關，2.intrinsic efficiency內在效率，就是偵測器接收訊號後能轉換放出的比例，3.偵測器放出訊號後，後端的記錄系統能真正記錄下來的比例，這部分跟能量選擇有一點關係，因為如果能量不對的話是會被剔除的，4.射源放出射線到偵檢器之間不被散射真正被吸收的比例，因此真正的偵測效率是以上4個因子相乘而得到的結果，題目現在問到的是第1個部分幾何效率，由於幾何效率約等於A/4πr2，其中r是與射源的距離，A是在那個距離時偵檢器所能涵蓋的範圍，簡單來講就是射源是呈球狀的向外發射，偵檢器在與射源距離為r時，那個球體的表面積是4πr2，所能真正包住的區域只有其中的一部份，也就是先前所假設的A，因此幾何效率就是偵測器能包覆住射源發射表面積的百分比，所包的區域越多，幾何效率越高，這也是井型計數器為什麼要做成井型的緣故，整個偵測器只留下要放檢體的那個洞，其他都是由閃爍晶體所包圍住，題目現在問的是counting geometry，翻成中文就是計數幾何，坦白講我不曉得這是在問什麼，不過因為因為選項中有(D)4π這個選項，因此我會猜它是正確答案。

56 用於放射免疫分析之碘-125 在伽傌計數器(gamma counter)進行偵測時，是利用何種機轉？ (A)Compton scattering (B)photoelectric effect (C)annihilation (D)以上皆非

伽傌計數器的構造如54題的圖，I-125所發射能量為35 KeV的γ-ray撞擊到NaI發光後，可見光再被光電倍增管接收放大後才能計數，因此是利用(B)photoelectric effect。

57 閃爍攝影機之敏感度為： (A)CPS(count per second) (B)C/MBq(count per mega Bq) (C)MBq/s(mega Bq per second) (D)CPS/MBq(count per second per mega Bq)

閃爍攝影機的系統敏感度會隨著所使用的準直儀不同而有所不同，一般來說要測量使用低能量準直儀時的敏感度會使用Tc-99m(140 KeV)，中能量準直儀會用In-111(172，247 KeV)，高能量則使用I-131(364 KeV)，測量的方法則是利用已知活度的核種置於直徑10公分的圓盤內，深度約2到3 mm，然後將這個射源置於準直儀上方10公分處收集影像，收集完畢後畫一個圓形的ROI包含住所收集到的影像來計算總count數，接著將射源移除以相同條件再收集一個影像作為背景值，這樣系統的敏感度就可以表示成[射源在ROI的count-BG的ROI]/[時間(sec)*射源活度(Bq)]，這樣計算結果的單位就會是count/(sec*Bq)，也就是CPS/Bq，答案(D)CPS/MBq(count per second per mega Bq)是將Bq換成MBq，這樣只有小數點位置的變化而已，單位是相同的，一般來說多功能型的準直儀的敏感度約在1~1.5*10 -4 cps/Bq或是0.01~0.015%左右。

58 FWHM(full width at half maximum)通常用來描述閃爍攝影機的何種性質？ (A)均勻度 (B)線性度 (C)解析度 (D)敏感度

這一題可以參考91年第1次高考第14題以及92年第1次高考第77題，如果將FWHM除以該能量的keV值就能夠算出儀器的能量解析力，因此FWHM可以用來描述閃爍攝影機的(C)解析度。

59 下面何種射線穿透組織之距離最短？ (A)α-射線 (B)β-射線 (C)γ-射線 (D)χ-射線

這個答案是(A)α-射線，我想應該是不用作什麼解釋才對吧。

60 閃爍攝影機的NaI(Tl)晶體作用為： (A)引導伽傌射線 (B)將伽傌射線轉變成能量 (C)將伽傌射線轉變成光線 (D)將伽傌射線轉變成電子訊號

這題請參考91年第2次檢覈考第33題和92年第1次高考第66題，NaI的作用是(C)將伽傌射線轉變成光線。